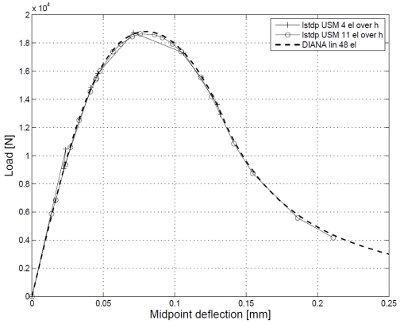
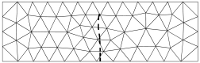
When modeling discrete cracks, as in e.g. reinforced concrete structures, steel structures, wind turbine blades or in glass structures, XFEM (the Extended Finite Element Method) is a very efficient modeling tool. XFEM makes it possible to model growing cracks without remeshing and it can model totally separated parts. The method was introduced in the late 90’ies by Belytschko and coworkers (Belytschko and Black, 1999). XFEM was originally formulated for LEFM (Linear Elastic Fracture Mechanics) (suitable for steel and glass) but since then formulations for Non-linear Fracture Mechanics (suitable for concrete and laminated structures) have been presented. Today XFEM has been formulated for many different applications including intersecting cracks, cracks in 3D and partly cracked elements. With the latest advancements within the area of partly cracked elements by Asferg et. al. 2007 and Mougaard et. al. 2009 a cracked concrete beam subjected to three point bending can be modeled using very few elements, see figure below.
Ongoing research in the group is concerned with:
-
Including crack length parameters in the model for efficient solving of the non-linear equations.
-
Arbitrarily intersecting cracks for modeling multiple cracking.
-
Partly cracked 3D elements for realistic modeling of cracked structures.
|
|
|
|
|
|
XFEM modelling of a beam in three point bending.
|
References
Belytschko, T. and Black, T., Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Meth. Engng. 1999, Vol. 45: 601-620.
Asferg, J.L., Poulsen, P.N. and Nielsen, L.O., A consistent partly cracked XFEM element for cohesive crack growth. Int. J. Numer. Meth. Engng. 2007, Vol. 72: 464-485.
Mougaard, J.F., Poulsen, P.N. and Nielsen, L.O., A partly and fully cracked XFEM element based on higher order polynomial shape functions for modeling cohesive fracture. Submitted for publication.